Ever wondered what the Towers of Hanoi puzzle looks like when solved step by step? I found this cool Haskell code that shows the solution as pictures. It’s really neat to watch the disks move around!

The Towers of Hanoi is that old puzzle with three pegs and some disks of different sizes. You have to move all disks from the left peg to the right peg, but you can only move one disk at a time and you can never put a bigger disk on top of a smaller one.

Here’s how the code works:

First, it picks some nice colors for the disks:

colors = cycle $ map sRGB24read [ "#9FB4CC", "#CCCC9F", "#DB4105", "#FFF8E3", "#33332D"]

Each disk gets a different color based on its size. The bigger disks are wider rectangles, which makes sense when you look at it.

To draw a single disk, it makes a rectangle with width based on the disk number:

renderDisk :: Disk -> Dia
renderDisk n = rect (fromIntegral n + 2) 1
               # lc black
               # lw thin
               # fc (colors !! n)

For a whole stack of disks, it just piles them up on top of a peg:

renderStack :: Stack -> Dia
renderStack s = disks `atop` post
  where disks = (vcat . map renderDisk $ s)
                # alignB
        post  = rect 0.8 6
                # lw none
                # fc black
                # alignB

The cool part happens in the solving. The algorithm uses recursion - that’s when a function calls itself. For n disks, it:

  1. Moves n-1 disks from the start to the middle peg
  2. Moves the biggest disk to the end
  3. Moves the n-1 disks from the middle to the end
solveHanoi :: Int -> [Move]
solveHanoi n = solveHanoi' n 0 1 2
  where solveHanoi' 0 _ _ _ = []
        solveHanoi' n a b c = solveHanoi' (n-1) a c b ++ [(a,c)]
                              ++ solveHanoi' (n-1) b a c

The doMove function actually does each move by taking a disk from one stack and putting it on another:

doMove :: Move -> Hanoi -> Hanoi
doMove (x,y) h = h''
  where (d,h')         = removeDisk x h
        h''            = addDisk y d h'
        removeDisk x h = (head (h!!x), modList x tail h)
        addDisk y d    = modList y (d:)

Finally, it makes a list of all the puzzle states and shows them stacked up and down:

renderHanoiSeq :: [Hanoi] -> Dia
renderHanoiSeq = vcat' (with & sep .~2) . map renderHanoi

Pretty cool how a few lines of code can show you exactly how an algorithm works, right? Sometimes the best way to understand something is to see it in action.

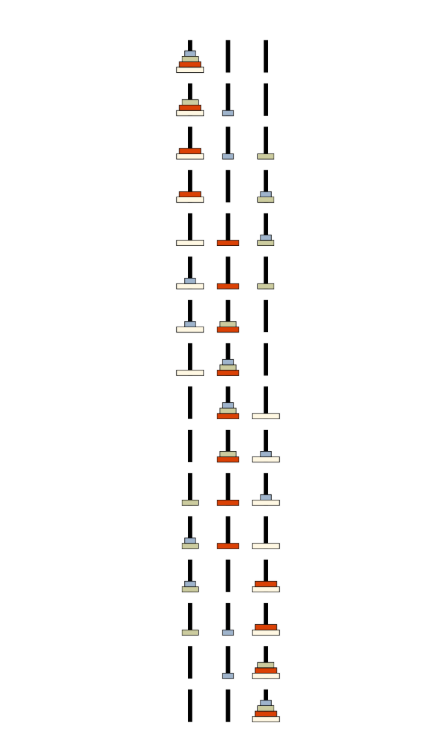
Towers of Hanoi Solution

Visualizing the classic Towers of Hanoi puzzle solution using Haskell and the Diagrams library.